The Kingdom of Childhood
GA 311
Lecture V
16 August 1924, Torquay
It will be essential for you to have some understanding of the real essence of every subject that you teach, so that you do not make use of things in your teaching that are remote from life itself. Everything which is intimately connected with life can be understood. One could even say that whatever one really understands has this intimate connection with the life of man. This is not the case with abstractions.
What we find today is that the ideas a teacher has are largely abstractions, so that in many respects he is himself remote from life. This brings very great difficulties into education and teaching. Just consider the following: Imagine that you want to think over how you first came to count things and what really happens when you count. You will probably find that the thread of your recollections breaks somewhere, and that you did once learn to count, but actually you do not really know what you do when you count.
Now all kinds of theories are thought out for the teaching of number and counting, and it is customary to act upon such theories. But even when external results can be obtained, one does not touch the whole being of the child with this kind of counting or with similar things that have no connection with real life. The modern age has proved that it lives in abstractions, by inventing such things as the abacus or bead-frame for teaching. In a business office people can use calculating machines as much as they like—that does not concern us at the moment, but in teaching, this calculating machine, which is exclusively concerned with the activities of the head, prevents one from the very start from dealing with number in a way which is in accordance with the child nature.
Counting however should be derived from life itself, and here it is supremely important to know from the beginning that we should not ever expect the child to understand every single thing we teach him. He must take a great deal on authority, but he must take it in a natural, practical way.
Perhaps you may find that what I am now going to say will be rather difficult for the child. But that does not matter. It is of great significance that there should be moments in a man's life when in his thirtieth or fortieth year he can say to himself: Now I understand what in my eighth or ninth year, or even earlier, I took on authority. This awakens new life in a man. But if you look at all the object lessons that are introduced into the teaching of today, you may well be in despair over the way things are made trivial, in order, as one says, to bring them nearer to the child's understanding.
Now imagine that you have quite a small child in front of you, one of the youngest, who is still quite clumsy in his movements, and you say to him: “You are standing there before me. Here I take a piece of wood and a knife, and I cut the wood into pieces. Can I do that to you?” The child will see for himself that I cannot do it to him. And now I can say to him: “Look, if I can cut the piece of wood in two, the wood is not like you, and you are not like the wood, for I cannot cut you in two like that. So there is a difference between you and the wood. The difference lies in the fact that you are a unit, a ‘one,’ and the wood is not a ‘one.’ You are a unit and I cannot cut you in two, and therefore I call you ‘one,’ a unit.”
You can now gradually proceed to show the child a sign for this “one.” You make a stroke: I, so that you show him it is a unit and you make this stroke for it.
Now you can leave this comparison between the wood and the child and you can say: “Look, here is your right hand but you have another hand too, your left hand. If you only had this one hand it could certainly move about everywhere as you do, but if your hand were only to follow the movement of your body you could never touch yourself in the way in which your two hands can touch each other. For when this hand moves and the other hand moves too at the same time, then they can take hold of each other, they can come together. That is different from when you simply move alone. In that you walk alone you are a unit. But the one hand can touch the other hand. This is no longer a unit, this is a duality, a ‘two.’ See, you are one, but you have two hands.” This you then show like this: II.
In this way you can work out a conception of the “one” and the “two” from the child's own form.
Now you call out another child and say: “When you two walk towards each other you can also meet and touch each other; there are two of you, but a third can join you. This is impossible with your hands.” Thus you can proceed to the three: III.
In this manner you can derive number out of what man is himself. You can lead over to number from the human being, for man is not an abstraction but a living being.
Then you can pass on and say: “Look, you can find the number two somewhere else in yourself.” The child will think finally of his two legs and feet. Now you say: “You have seen your neighbour's dog, haven't you? Does he only go on two feet also?” Then he will come to realise that the four strokes IIII are a picture of the neighbour's dog propped up on four legs, and thus he will gradually learn to build up number out of life.
The teacher must have his eyes open wherever he goes and look at everything with understanding. Now we naturally begin to write numbers with the Roman figures, because these of course will be immediately understood by the child, and when you have got to the four you will easily be able, with the hand, to pass over to five—V. You will soon see that if you keep back your thumb you can use this four as the dog does!: I I I I. Now you add the thumb and make five—V.
I was once with a teacher who had got up to this point (in explaining the Roman figures) and could not see why it occurred to the Romans not to make five strokes next to one another but to make this sign V for the five. He got on quite well up to I I I I. Then I said: “Now let us do it like this: Let us spread out our fingers and our thumb so that they go in two groups, and there we have it, V. Here we have the whole hand in the Roman five and this is how it actually originated. The whole hand is there within it.”
In a short lecture course of this kind it is only possible to explain the general principle, but in this way we can derive the idea of number from real life, and only when number has thus been worked out straight from life should you try to introduce counting by letting the numbers follow each other. But the children should take an active part in it. Before you come to the point of saying: Now tell me the numbers in order, 1, 2, 3, 4, 5, 6, 7, 8, 9 and so on, you should start with a rhythm; let us say we are going from 1 to 2, then it will be: 1, 2; 1, 2; 1, 2; let the child stamp on 2 and then on to 3 also in rhythm: 1, 2, 3; 1, 2, 3. In this way we bring rhythm into the series of numbers, and thereby too we foster the child's faculty of comprehending the thing as a whole. This is the natural way of teaching the children numbers, out of the reality of what numbers are. For people generally think that numbers were thought out by adding one to the other. This is quite untrue, for the head does not do the counting at all. In ordinary life people have no idea what a peculiar organ this human head really is, and how useless for our earthly life. It is there for beauty's sake, it is true, because our faces please each other. It has many other virtues too, but as far as spiritual activities are concerned it is really not nearly so much in evidence, for the spiritual qualities of the head always lead back to man's former earth-life. The head is a metamorphosis of the former life on earth, and the fact of having a head only begins to have a real meaning for man when he knows something of his former earth lives. All other activities come from somewhere else, not from the head at all. The truth is that we count subconsciously on our fingers. In reality we count from 1-1 o on our ten fingers, then eleven (adding the toes), twelve, thirteen, fourteen (counting on the toes). You cannot see what you are doing, but you go on up to twenty. And what you do in this manner with your fingers and toes only throws its reflection into the head. The head only looks on at all that occurs. The head in man is really only an apparatus for reflecting what the body does. The body thinks, the body counts. The head is only a spectator.
We can find a remarkable analogy for this human head. If you have a car and are sitting comfortably inside it, you are doing nothing yourself; it is the chauffeur in front who has to exert himself. You sit inside and are driven through the world. So it is with the head; it does not toil and moil, it simply sits on the top of your body and lets itself be carried quietly through the world as a spectator. All that is done in spiritual life is-done from the body. Mathematics are done by the body, thinking is also done by the body, and feeling too is done with the body. The bead-frame has arisen from the mistaken idea that man reckons with his head. Sums are then taught to the child with the bead-frame, that is to say, the child's head is made to work and then the head passes on the work to the body, for it is the body which must do the reckoning. This fact, that the body must do the reckoning, is not taken into account, but it is important. So it is right to let the child count with his fingers and also with his toes, for indeed it is good to call forth the greatest possible skill in the children. In fact there is nothing better in life than making the human being skilful in every way. This cannot be done through sport, for sport does not really make people skilled. What does make a man skilled is to give him a pencil, for instance, and let him hold it between his big toe and the next toe and learn to write with his foot, to write figures with his foot. This can be of real significance, for in truth man is permeated with soul and spirit in his whole body. The head is the traveller that sits back restfully inside and does nothing, whilst the body, every part of it, is the chauffeur who has to do everything.
Thus from the most varied sides you must try to build up what the child has to learn as counting. And when you have worked in this way for a time it is important to pass on and not merely take counting by adding one thing to another; indeed this is the least important aspect of counting and you should now teach the child as follows: “This is something which is ONE. Now you divide it like this, and you have something which is TWO. It is not two ONEs put together but the two come out of the ONE.” And so on with three and four. Thus you can awaken the thought that the ONE is really the comprehensive thing that contains within itself the TWO, the THREE, the FOUR, and if you learn to count in the way indicated in the diagram, 1, 2, 3, 4 and so on, then the child will have concepts that are living. He thereby comes to experience something of what it is to be inwardly permeated with the element of number.
In bygone ages our present conceptions of counting by placing one bean beside another or one bead beside another in the frame were quite unknown; in those days it was said that the unit was the largest, every two is only the half of it, and so on. So you come to understand the nature of counting
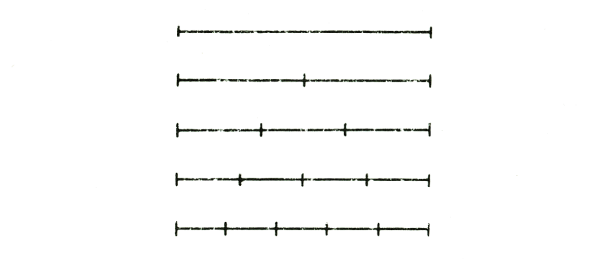
by actually looking at external objects. You should develop the child's thinking by means of external things which he can see, and keep him as far away as possible from abstract ideas.
The children can then gradually learn the numbers up to a certain point, first, let us say, up to twenty, then up to a hundred and so on. If you proceed on these lines you will be teaching the child to count in a living way. I should like to emphasise that this method of counting, real counting, should be presented to the child before he learns to do sums. The child ought to be familiar with this kind of counting before you go on to Arithmetic.
Arithmetic too must be approached out of life. The living thing is always a whole and must be presented as a whole first of all. You are doing wrong to a child if you always make him put together a whole out of its parts, and do not teach him to look first at the whole and then divide this whole into its parts; get him first to look at the whole and then divide it and split it up; this is the right path to a living conception.
Many things that the materialistic epoch has done with regard to the general culture of mankind pass unnoticed. Nowadays no one is scandalised but regards it rather as a matter of course to let children play with boxes of bricks, and build things out of the single blocks. This of itself leads them away from what is living. The child out of his very nature has no impulse to put together a whole out of parts. He has many other needs and impulses which are, admittedly, much less convenient. If you give him a watch for instance, he immediately has the desire to pull it to pieces, to break up the whole into its parts, which is actually far more in accordance with the nature of man—to see how the whole arises out of its component parts.
This is what must now be taken into account in our Arithmetic teaching. It has an influence on the whole of culture, as you will see from the following example.
In the conception of human thought up to the thirteenth and fourteenth centuries very little emphasis was laid upon putting together a whole out of its parts; this arose later. The master-builder built much more from the idea of the whole (which he then split up into its parts) rather than starting with the single parts and making a building out of these. The latter procedure was really only introduced into civilisation later on. This conception then led to people thinking of every single thing as being put together out of the very smallest parts. Out of this arose the atomic theory in Physics, which really only comes from education. For atoms are really tiny little caricatures of demons, and our learned scholars would not speak about them as they do unless people had grown accustomed, in education, to putting everything together out of its parts. Thus it is that atomism has arisen.
We criticise atomism today, but criticism is really more or less superfluous because men cannot get free from what they have been used to thinking of wrongly for the last four or five centuries; they have become accustomed to go from the parts to the whole instead of letting their thoughts pass from the whole to the parts.
This is something we should particularly bear in mind in the teaching of Arithmetic. If you are walking towards a distant wood you first see the wood as a whole, and only when you come near it do you perceive that it is made up of single trees. This is just how you must proceed in Arithmetic. You never have in your purse, let us say, 1, 2, 3, 4, 5 coins, but you have a heap of coins. You have all five together, which is a whole. This is what you have first of all. And when you cook pea soup you do not have 1, 2, 3, 4, 5 or up to 3o or 4o peas, but you have one heap of peas, or with a basket of apples, for instance, there are not 1, 2, 3, 4, 5, 6, 7 apples, but one heap of apples in your basket. You have a whole. What does it matter to us to begin with, how many we have? We simply have a heap of apples which we are now bringing home (see diagram). There are, let us say, three children. We

will not now divide them so that each gets the same, for perhaps one child is small, another big. We put our hand into the basket and give the bigger child a bigger handful, the. smaller child a smaller handful; we divide our heap of apples into three parts.
Dividing or sharing out is in any case such a queer business! There was once a mother who had a large piece of bread. She said to her little boy, Henry: “Divide the bread, but you must divide it in a Christian way.” Then Henry said: “What does that mean, divide it in a Christian way?” “Well,” said his mother, “You must cut the bread into two pieces, one larger and one smaller; then you must give the larger piece to your sister Anna and keep the smaller one for yourself.” Whereupon Henry said, “Oh well, in that case let Anna divide it in a Christian way!”
Other conceptions must come to your aid here. We will do it like this, that we give this to one child, let us say {see lines in the drawing), and this heap to the second child, and this to the third. They have already learnt to count, and so that we get a clear idea of the whole thing we will first count the whole heap. There are eighteen apples. Now I have to count up what they each have. How many does the first child get? Five. How many does the second child get? Four. And the third? Nine. Thus I have started from the whole, from the heap of apples, and have divided it up into three parts.
Arithmetic is often taught by saying: “You have five, and here is five again and eight; count them together and you have eighteen.” Here you are going from the single thing to the whole, but this will give the child dead concepts. He will not gain living concepts by this method. Proceed from the whole, from the eighteen, and divide it up into the addenda; that is how to teach addition.
Thus in your teaching you must not start with the single addenda, but start with the sum, which is the whole, and divide it up into the single addenda. Then you can go on to show that it can be divided up differently, with different addenda, but the whole always remains the same. By taking addition in this way, not as is very often done by having first the addenda and then the sum, but by taking the sum first and then the addenda, you will arrive at conceptions that are living and mobile. You will also come to see that when it is only a question of a pure number the whole remains the same, but the single addenda can change. This peculiarity of number, that you can think of the addenda grouped in different ways, is very clearly brought out by this method.
From this you can then proceed to show the children that when you have something that is not itself a pure number but that contains number within it, as the human being for example, then you cannot divide it up in all these different ways. Take the human trunk for instance and what is attached to it, head, two arms and hands, two feet; you cannot now divide up the whole as you please; you cannot say: now I will cut out one foot like this, or the hand like this, and so on, for it has already been membered by nature in a definite way. When this is not the case, and it is simply a question of pure counting, then I can divide things up in different ways.
Such methods as these will make it possible for you to bring life and a kind of living mobility into your work. All pedantry will disappear and you will see that something comes into your teaching that the child badly needs: humour comes into the teaching, not in a childish but in a healthy sense. And humour must find its place in teaching.1At this. point Dr. Steiner turned to the translator and said: “Please be sure you translate the word ‘humour’ properly, for it is always misunderstood in connection with teaching!”
This then must be your method: always proceed from the whole. Supposing you had such an example as the following, taken from real life. A mother sent Mary to fetch some apples. Mary got twenty-five apples. The apple-woman wrote it down on a piece of paper. Mary comes home and brings only ten apples. The fact is before us, an actual fact of life, that Mary got twenty-five apples and only brought home ten. Mary is an honest little girl, and she really didn't eat a single apple on the way, and yet she only brought home ten. And now someone comes running in, an honest person, bringing all the apples that Mary dropped on the way. Now there arises the question: How many does he bring? We see him coming from a distance, but we want to know beforehand how many he is going to bring. Mary has come home with ten apples, and she got twenty-five, for there it is on the paper written down by the apple-woman, and now we want to know how many this person ought to be bringing, for we do not yet know if he is honest or not. What Mary brought was ten apples, and she got twenty-five, so she lost fifteen apples..
Now, as you see, the sum is done. The usual method is that something is given and you have to take away something else, and something is left. But in real life—you may easily convince yourselves of this—it happens much more often that you know what you originally had and you know what is left over, and you have to find out what was lost. Starting with the minuend and the subtrahend and working out the remainder is a dead process. But if you start with the minuend and the remainder and have to find the subtrahend, you will be doing subtraction in a living way. This is how you may bring life into your teaching.
You will see this if you think of the story of Mary and her mother and the person who brought the subtrahend; you will see that Mary lost the subtrahend from the minuend and that has to be justified by knowing how many apples the person you see coming along will have to bring. Here life, real life, comes into your subtraction. If you say, so much is left over, this only brings something dead into the child's soul. You must always be thinking of how you can bring life, not death, to the child in every detail of your teaching.
You can continue in this method. You can do multiplication by saying: “Here we have the whole, the product. How can we find out how many times something is contained in this product?” This thought has life in it. Just think how dead it is when you say: I will divide up this whole group of people, here are three, here are three more and so on, and now I ask: how many times three have we here? That is dead, there is no life in it.
If I proceed the other way round and take the whole and ask how often one group is contained within it, then I bring life into it. I can say to the children for instance: “Look, there is a certain number of you here in the class. Let us count. There are forty-five of you in the class. Now I am going to choose out five, 1, 2, 3, 4, 5 and put them over here.” Then I let them count up; how many times are these five contained within the forty-five? You see that here again I consider the whole and not the part. How many more of these groups of five can I make? Then I find out that there are eight more groups of five. Thus I do the thing the other way round and start with the whole, the product, and find out how often one factor is contained in it. Thereby I bring life into my arithmetical methods and above all I begin with something that the child can see before him. The chief point is that we must never, never separate thinking from visual experience, from what the child can see, for otherwise we shall bring intellectualism and abstractions to the child in early life and thereby ruin his whole being. He will become dried up and this will not only affect the soul life but the physical body also, causing desiccation and sclerosis. (We shall later have to speak of the education of spirit, soul and body as a unity.)
Here again much depends on our teaching Arithmetic in the way we have considered, so that in old age the human being is still mobile and skilful. You should teach the children to count from their own bodies as I have described, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, first with the fingers and then with the toes—yes indeed, it would be good to accustom the children actually to count up to twenty with their fingers and toes, not on a bead-frame. If you teach them thus then you will see that through this childlike kind of “meditation” you are bringing life into the body; for when you count on your fingers or toes you have to think about these fingers and toes, and this is then a meditation, a healthy kind of meditating on one's own body. If this is done a man will still be able to use his limbs skilfully in old age; the limbs can still function fully because they have learnt to count by way of the whole body. If a man only thinks with his head, rather than with his limbs and the rest of his organism, then later on the limbs lose their function and gout sets in.
This principle, that everything in teaching and education must be worked out from what can be seen (but not from what are often called “object lessons” today)—this principle I should like to illustrate for you with an example, something which can actually play a very important part in teaching. I am referring to the Theorem of Pythagoras which as would-be teachers you must all be well acquainted with, and which you may even have already come to understand in a similar way; but we will speak of it again today. Now the Theorem of Pythagoras can be taken as a kind of goal in the teaching of Geometry. You can build up your Geometry lessons to reach their climax, their summit, in the Theorem of Pythagoras, which states that the square on the hypotenuse of a right-angled triangle is equal to the sum of the squares on the other two sides. It is a marvellous thing if we see it in the right light.
I once had to teach Geometry to an elderly lady because she loved it so much; she may have forgotten everything, I do not know, but she had probably not learnt much at her school, one of those schools for the “Education of Young Ladies.” At all events she knew no Geometry at all, so I began and made everything lead up to the Theorem of Pythagoras which the old lady found very striking. We are so used to it that it no longer strikes us so forcibly, but what we have to understand is simply that if I have a right-angled triangle here (see diagram) the area of the square on the hypotenuse is equal to the sum of the other two areas, the two squares on the other two sides. So that if I am planting potatoes and put them at the same distance from each other everywhere, I shall plant the same number of potatoes in the two smaller fields together as in the larger one. This is something very remarkable, very striking, and when you look at it like this you cannot really see how it comes about.
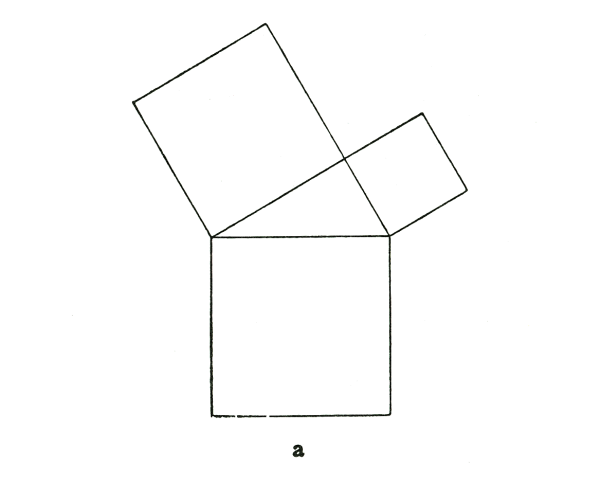
It is just this fact of the wonder of it, that you cannot see how it comes about, that you must make use of to bring life into the more inward, soul quality of your teaching; you must build on the fact that here you have something that is not easily discernible; this must constantly be acknowledged. One might even say with regard to the Theorem of Pythagoras that you can believe it, but you always have to lose your belief in it again. You have to believe afresh every time that this square is equal to the sum of the other two squares.
Now of course all kinds of proofs can be found for this, but the proof ought to be given in a clear visual way. (Dr. Steiner then built up a proof for the Theorem of Pythagoras in detail based on the superposition of areas; he gave it in the conversational style used in this Lecture Course, and with the help of the blackboard and coloured chalks. For those who are interested a verbatim report of this proof, with diagrams, can be found in the Appendix on page 106.)
If you use this method of proof, i.e. laying one area over the other, you will discover something. If you cut it out instead of drawing it you will see that it is quite easy to understand. Nevertheless, if you think it over afterwards you will have forgotten it again. You must work it out afresh every time. You cannot easily hold it in your memory, and therefore you must rediscover it every time. That is a good thing, a very good thing. It is in keeping with the nature of the Theorem of Pythagoras. One must arrive at it afresh every time. One should always forget that one has understood it. This belongs to the remarkable quality of the Theorem of Pythagoras itself, and thereby you can bring life into it. You will soon see that if you make your pupils do it again and again, they have to ferret it out by degrees. They do not get it at once, they have to think it out each time. But this is in accordance with the inner living quality of the Theorem of Pythagoras. It is not good to give a proof that can be understood in a flat, dry kind of way; it is much better to forget it again constantly and work it out every time afresh. This is inherent in the very wonder of it, that the square on the hypotenuse is equal to the squares on the other two sides.
With children of eleven or twelve you can quite well take Geometry up to the point of explaining the Theorem of Pythagoras by this comparison of areas, and the children will enjoy it immensely when they have understood it. They will be enthusiastic about it, and will always be wanting to do it again, especially if you let them cut it out. There will perhaps be a few intellectual good-for-nothings who remember it quite well and can always do it again. But most of the children, being more reasonable, will cut it out wrong again and again and have to puzzle it out till they discover how it has to go. That is just the wonderful thing about the Theorem of Pythagoras, and we should not forsake this realm of wonder but should remain within it.
APPENDIX TO LECTURE 5
I. Proof for the Theorem of Pythagoras.
(As it has been impossible to reproduce the diagrams in colour, the forms which Dr. Steiner referred to by their colours have been indicated by letters or numbers.) It is quite easy to do this proof if the triangle is isosceles. If you have here a right-angled isosceles triangle (see diagram a.), then this is one side, this is the other and this the hypotenuse. This square (1, 2, 3, 4) is the square on the hypotenuse. The squares (2, 5) and (4, 6) are the squares on the other two sides.
Now if I plant potatoes evenly in these two fields (2, 5) and (4, 6), I shall get just as many as if I plant potatoes in
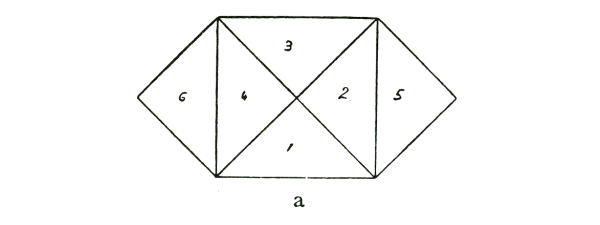
this field (1, 2, 3, 4). (1, 2, 3, 4) is the square on the hypotenuse, and the two fields (2, 5) and (4, 6) are the squares on the other two sides.
You can make the proof quite obvious by saying: the parts (2) and (4) of the two smaller squares fall into this space here (1, 2, 3, 4, the square on the hypotenuse); they are already within it. The part (5) exactly fits in to the space (3), and if you cut out the whole thing you can take the triangle (6) and apply it to (1), and you will see at once that it is the same. So that the proof is quite clear if you have a so-called right-angled isosceles triangle.
If however you have a triangle that is not isosceles, but has unequal sides (see diagram b.), you can do it as follows:
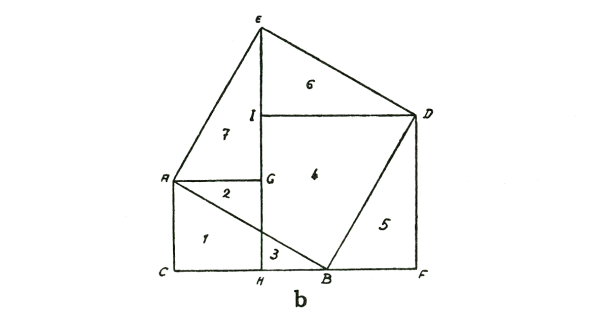
draw the triangle again ABC; then draw the square on the hypotenuse ABDE. Proceed as follows: draw the triangle ABC again over here, DBF. Then this triangle ABC or DBF (which is the same), can be put up there, AGE. Since you now have this triangle repeated over there, you can draw the square over one of the other sides, CAGH.
As you see, I can now also draw this triangle DEI congruent to BCA. Then the square DIHF is the square on the other side. Here I have both the square on the one side and the square on the other side. In the one case I use the side AG and in the other case the side DI. The two triangles AEG and DEI are congruent. Where is then the square on the hypotenuse? It is the square ABDE. Now I have to show from the figure itself that (1, 2) and (3, 4, 5) together make up (2, 4, 6, 7). Now I first take the square (1, 2); this has the triangle (2) in common with the square on the hypotenuse ABDE and section (4) of the square on the other side HIDF is also contained in ABDE. Thus I get this figure (2, 4) which you see drawn here and which is actually a piece of the square ABDE. This only leaves parts (1, 3 and 5) of the squares AGHC and DIHF to be fitted into the square on the hypotenuse ABDE. Now you can take part (5) and lay it over part (6), but you will still have this corner (1, 3) left over. If you cut this out you will discover that these two areas (1, 3) fit into this area (7). Of course it can be drawn more clearly but I think you will understand the process.

